I - Kuririn MIRACLE
基本信息
| 题目出处 | 2018 ICPC 亚洲区域赛青岛站网络赛 |
| 队伍通过率 | 7/1550 (0.5%) |
题解
记第一辆车的圆心为 \(A\),第二辆车(障碍物)的圆心为 \(B\)。首先容易想到答案的上界:圆 \(A\) 就跟在圆 \(B\) 后面沿 \(x\) 轴走到终点,时间是 \(\frac{d}{v}\)。
由于圆 \(A\) 的速度比圆 \(B\) 快,也可以先让圆 \(A\) 与圆 \(B\) 保持相切,从圆 \(B\) 上方绕过去,绕到某个角度后,再沿直线走到终点。接下来我们分别计算两段路径的时间。
第一段路径
点 \(A\) 的第一段运动可以拆分成跟着圆 \(B\) 的,速度为 \(v\) 的匀速直线运动,和绕着圆 \(B\) 的,半径为 \(2r\) 的变速圆周运动。
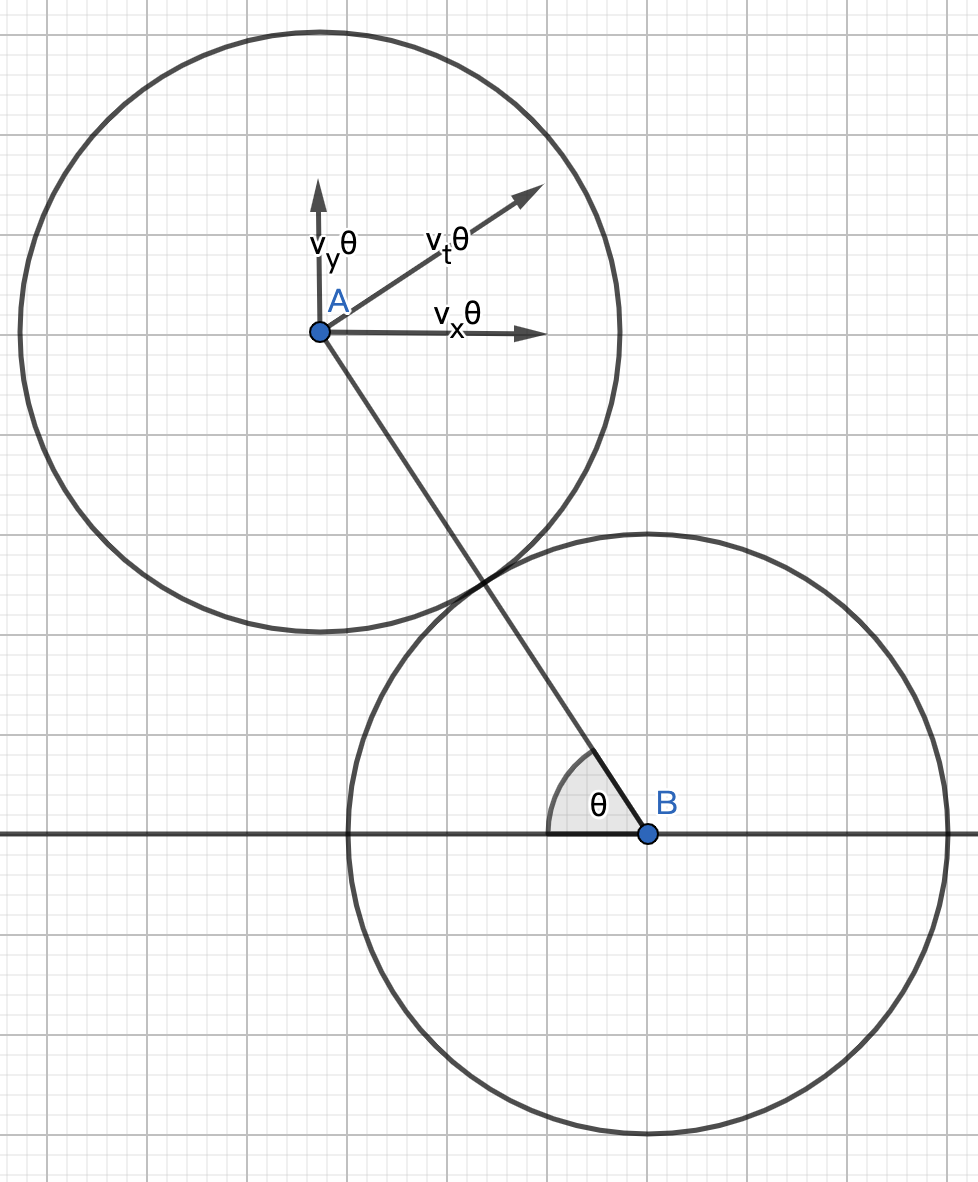
如上图所示,记 \(AB\) 和 \(x\) 轴负方向的夹角为 \(\theta\),点 \(A\) 相对点 \(B\) 的切向速度为 \(v_t(\theta)\),\(v_x(\theta)\) 是 \(v_t(\theta)\) 沿 \(x\) 轴正方向的分解速度,\(v_y(\theta)\) 是 \(v_t(\theta)\) 沿 \(y\) 轴正方向的分解速度,有以下方程组。
\[
\begin{cases}
v_x(\theta) = v_t(\theta)\sin \theta \\
v_y(\theta) = v_t(\theta)\cos \theta \\
(v_x(\theta) + v) ^ 2 + (v_y(\theta))^2 = (2v)^2
\end{cases}
\]
解得 \(v_t(\theta) = v (\sqrt{\sin^2\theta + 3} - \sin\theta)\)。
设第一段运动一直持续到 \(\theta = \alpha\),则根据弧长公式,第一段运动的用时为
\[
t = \int_{0}^{\alpha} \frac{2rd\theta}{v_t(\theta)}
\]
这个积分没有代数解,可以使用 自适应辛普森公式 近似计算。
第二段路径
当点 \(A\) 经过第一段路径后,坐标为
\[
\begin{cases}
x = vt + 2r - 2r\cos \alpha \\
y = 2r\sin \alpha
\end{cases}
\]
接下来,点 \(A\) 将从这个坐标向终点做匀速直线运动,因此第二段运动的用时为 \(\frac{\sqrt{(x - d)^2 + y^2}}{2v}\)。
剩下的问题就是如何确定 \(\alpha\) 的值。设第二段路径开始前,点 \(A\) 和终点的连线与 \(x\) 轴负方向的夹角为 \(\beta\)。考虑以点 \(B\) 为中心的参考系,点 \(A\) 在该参考系中将从 \(\vec{a} = (x - (2r + vt), y)\) 出发,沿 \(\vec{w} = (2v\cos \beta - v, -2v\sin \beta)\) 方向做匀速直线运动。为了保证 \(AB\) 两点之间的距离不缩小,向量 \(\vec{a}\) 和 \(\vec{w}\) 之间的夹角不能超过 \(90\) 度,即 \(\vec{a} \cdot \vec{w} \ge 0\)。二分 \(\alpha\) 的值并检查即可。
复杂度是二分的复杂度乘以辛普森公式的复杂度。
参考代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68 | #include <bits/stdc++.h>
#define EPS 1e-9
using namespace std;
double v, r, d;
int sgn(double x) {
if (x > EPS) return 1;
if (x < -EPS) return -1;
return 0;
}
// --------------------
// 辛普森公式
// --------------------
double f(double x) {
double s = sin(x);
return 1 / (sqrt(s * s + 3) - s);
}
double simpson(double l, double r) {
double mid = (l + r) / 2;
return (r - l) * (f(l) + 4 * f(mid) + f(r)) / 6;
}
double calc(double l, double r, double eps, double ans) {
double mid = (l + r) / 2;
double fl = simpson(l, mid), fr = simpson(mid, r);
if (abs(fl + fr - ans) <= 15 * eps) return fl + fr + (fl + fr - ans) / 15;
return calc(l, mid, eps / 2, fl) + calc(mid, r, eps / 2, fr);
}
// --------------------
// 辛普森公式结束
// --------------------
void solve() {
scanf("%lf%lf%lf", &v, &r, &d);
// 直接跟在圆 B 后面走到终点
double ans = d / v;
const double PI = acos(-1);
// 二分第一段运动结束时的角度
double head = PI / 2, tail = PI;
while (tail - head > EPS) {
double mid = (head + tail) / 2;
double t = 2 * r / v * calc(0, mid, EPS, simpson(0, mid));
double x = 2 * r * (1 - cos(mid)) + v * t;
double y = 2 * r * sin(mid);
double beta = atan2(y, d - x);
// 计算点乘的结果是否非负
double dot = (x - (2 * r + v * t)) * (2 * v * cos(beta) - v) - y * (2 * v * sin(beta));
if (sgn(dot) >= 0) {
tail = mid;
ans = min(ans, t + sqrt((x - d) * (x - d) + y * y) / (2 * v));
} else {
head = mid;
}
}
printf("%.9f\n", ans);
}
int main() {
int tcase; scanf("%d", &tcase);
while(tcase--) solve();
return 0;
}
|
