H - Mirror

Basic Information

Contest	The 2018 ICPC Asia Qingdao Regional Contest
Team AC Ratio	0/373 (0.0%)

Tutorial

We first deal with some special cases.

• If the segment connecting the start and end points has no obstacles, the answer is \((2m - 1) \times l\), where \(l\) is the distance between the start and end points.
• Otherwise, if \(m = 1\), we only need to consider the shortest path from the start to the end, avoiding obstacles and mirrors, no need to consider whether the path can see the start or end points. Therefore, we only need to consider the graph consisting of these seven points: start, end, obstacle vertices, and mirror endpoints, and compute the shortest path from the start to the end.
• Otherwise, \(m > 1\). This requires the existence of a route from the start to the end that can see both the start and end points at any point on the route. If either the start or end point is to the left of the mirror, without loss of generality let's assume that the end point is to the left of the mirror, then it will be impossible to see the start point from the end point, because the segment connecting the start and end points has an obstacle, and the end point cannot see the mirror. Therefore, this case has no solution.

After excluding the above special cases, the remaining case is: \(m > 1\), there are obstacles on the segment connecting the start and end points, and both points are to the right of the mirror.

At this point, the optimal route will be divided into three parts:

• At the beginning, we move the first stone from the start to the end, through a route where the start point can be seen at any time.
• In the middle, we need a route which is able to see the start and end points at any time, and this path will be repeated \((2m-3)\) times.
• Finally, we move the last stone from the start to the end, through a route where the end point can be seen at any time.

Therefore, we need to consider which lines, as they are crossed, may change the visibility of the start and end points. A graph is built based on the intersection points of these lines. We need to calculate the length of the segment between any two points, whether there are obstacles on the segment, and whether each point on the segment can see the start and end points. Finally, the shortest path from the start to the end is calculated under specific visibility requirements.

The lines that cause changes in visibility are:

1. The line connecting the start/end point and the obstacle vertex.
2. The line connecting the start/end point and the mirror endpoint.
3. The line connecting the mirror image of the start/end point and the mirror endpoint.
4. The line connecting the mirror image of the start/end point and the obstacle vertex.
5. The line connecting the mirror image of the start/end point and the mirror image of the obstacle vertex.

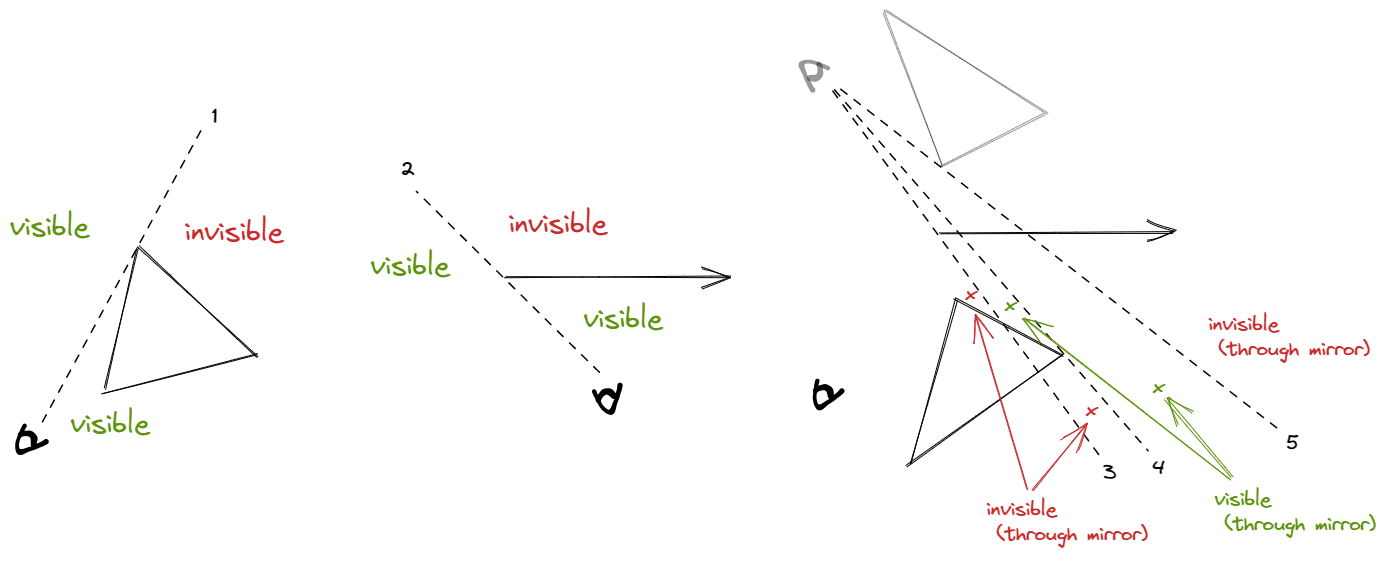
You may think that the boundary of the obstacle and the mirror will also change the visibility, why not consider them? Because a valid path cannot cross the boundary of the obstacle or mirror, there is no need to consider them.

When calculating whether each point on the segment between two points can always see the start and end points, since the segment may cross multiple lines that change the visibility, it is necessary to find the intersection points of the segment with each line and check the visibility of the midpoint of adjacent intersection points. This is correct because the region enclosed by the visibility lines is convex.

There is also an optimization for this problem: in fact, the optimal route is always on the right side of the mirror, so all points on the mirror line and to the left of it can be excluded, and only the points on the right side of the mirror need to be considered. We now roughly calculate the number of points we need to consider. Notice that the \(1\)-st type and the \(5\)-th type of lines are symmetrical, also the \(2\)-nd type and the \(3\)-rd type of lines are symmetrical. So the number of intersections of these lines on the right of the mirror is \(5 \times (15 + 10 + 5) \div 2 = 75\). Even if the intersections of the \(4\)-th type of lines are all on the right of mirror, the number of points to consider will be at most \(75 + 3 \times 18 + 3 \times 10 = 159\). Adding the start and end points, there will be \(161\) points.

So the time complexity is \(\mathcal{O}(n^2t + n^2\log n)\), where \(n = 161\) is the number of points to consider, and \(t = 26\) is the number of lines to change visibility.

Solution

#include <bits/stdc++.h>
#define MAXN 200
using namespace std;
typedef long double db;

const db eps = 1e-12;
const db inf = 1.0 / 0.0;

int sgn(db x) {
    if (x > eps) return 1;
    else if (x < -eps) return -1;
    else return 0;
}

struct Point {
    db x, y;

    Point() {}
    Point(db x, db y): x(x), y(y) {}

    db len() const {
        return sqrt(x * x + y * y);
    }

    Point operator +(const Point &p) const {
        return Point(x + p.x, y + p.y);
    }

    Point operator -(const Point &p) const {
        return Point(x - p.x, y - p.y);
    }

    Point operator *(db k) const {
        return Point(x * k, y * k);
    }

    Point operator /(db k) const {
        return Point(x / k, y / k);
    }

    db operator *(const Point &p) const {
        return x * p.y - p.x * y;
    }

    db operator ^(const Point &p) const {
        return x * p.x + y * p.y;
    }

    bool operator <(const Point &p) const {
        return sgn(x - p.x) < 0 || (sgn(x - p.x) == 0 && sgn(y - p.y) < 0);
    }

    bool operator ==(const Point &p) const {
        return sgn(x - p.x) == 0 && sgn(y - p.y) == 0;
    }
};

struct Line {
    Point s, t;

    Line() {}
    Line(Point s, Point t): s(s), t(t) {}

    db intersectRatio(const Line &l) const {
        if (sgn((t - s) * (l.t - l.s)) == 0) return inf;
        db u = (l.s - s) * (l.t - l.s), v = (t - s) * (l.t - l.s);
        return u / v;
    }

    vector<Point> operator &(const Line &l) const {
        db r = intersectRatio(l);
        if (r == inf) return {};
        return {s + (t - s) * r};
    }

    Point reflect(const Point &p) const {
        db u = ((p - s) ^ (t - s)), v = (t - s).len();
        return (s + (t - s) * (u / v / v)) * 2 - p;
    }

    db len() const {
        return sqrt((s.x - t.x) * (s.x - t.x) + (s.y - t.y) * (s.y - t.y));
    }
};

int X;
// s, t: start and end points
// m1, m2: endpoints of mirror
// a[i]: obstacle vertices
Point s, t, m1, m2, a[3];
// poly[i]: an edge of the obstacle polygon
Line poly[3];

// ms, mt: mirror image of start and end points
// ma[i]: mirror image of obstacle vertices
Point ms, mt, ma[3];
// mr: mirror
// mpoly[i]: mirror image of an edge of the obstacle polygon
Line mr, mpoly[3];

// calculate if segment l1 and l2 intersect
// `strict` means if they're strictly intersecting
// (if `strict == true` then intersecting on endpoints are not counted)
bool segmentIntersect(Line &l1, Line &l2, bool strict) {
    db r1 = l1.intersectRatio(l2), r2 = l2.intersectRatio(l1);
    if (strict) return sgn(r1) > 0 && sgn(r1 - 1) < 0 && sgn(r2) > 0 && sgn(r2 - 1) < 0;
    else return sgn(r1) >= 0 && sgn(r1 - 1) <= 0 && sgn(r2) >= 0 && sgn(r2 - 1) <= 0;
}

// check if segment l strictly intersects with obstacle or mirror
bool check(Line &l) {
    for (int i = 0; i < 3; i++) if (segmentIntersect(l, poly[i], true)) return false;
    if (segmentIntersect(l, mr, true)) return false;
    return true;
}

int n;
vector<int> e[MAXN], msk[MAXN];
vector<db> v[MAXN];
db dis[MAXN];

db dijkstra(int MSK) {
    for (int i = 0; i < n; i++) dis[i] = inf;
    typedef pair<db, int> pdi;
    priority_queue<pdi> pq;
    pq.push(pdi(0, 0));
    while (!pq.empty()) {
        pdi p = pq.top(); pq.pop();
        int sn = p.second;
        if (dis[sn] < inf) continue;
        dis[sn] = -p.first;
        for (int i = 0; i < e[sn].size(); i++) {
            int fn = e[sn][i];
            if ((MSK & msk[sn][i]) == MSK)
                pq.push(pdi(-dis[sn] - v[sn][i], fn));
        }
    }
    return dis[1];
}

// building graph of special case #2
// we only consider shortest paths among start/end points, obstacle vertices and mirror endpoints
// no need to consider visibility
void build1() {
    vector<Point> keys;
    keys.push_back(s); keys.push_back(t);
    keys.push_back(m1); keys.push_back(m2);
    for (int i = 0; i < 3; i++) keys.push_back(a[i]);

    n = keys.size();
    for (int i = 0; i < n; i++) e[i].clear(), v[i].clear(), msk[i].clear();
    for (int i = 0; i < n; i++) for (int j = i + 1; j < n; j++) {
        Line l(keys[i], keys[j]);
        if (!check(l)) continue;
        e[i].push_back(j); v[i].push_back(l.len()); msk[i].push_back(0);
        e[j].push_back(i); v[j].push_back(l.len()); msk[j].push_back(0);
    }
}

// if point `p` can see point `goal` directly or through mirror
bool visible(Point &p, Point &goal) {
    // see directly
    Line l = Line(p, goal);
    if (check(l)) return true;
    // see through mirror
    l = Line(p, mr.reflect(goal));
    // if we want to see through mirror,
    // then the segment connecting `p` and mirror image of `goal` must not intersect with
    // obstacle or mirror image of obstacle
    if (!segmentIntersect(l, mr, false)) return false;
    for (int i = 0; i < 3; i++) {
        if (segmentIntersect(l, poly[i], true)) return false;
        if (segmentIntersect(l, mpoly[i], true)) return false;
    }
    return true;
}

// if all points on segment `l` can see point `goal`
// border: the lines which change visibility
int visible(Line &l, Point &goal, vector<Line> &border) {
    typedef pair<db, Point> pdp;
    vector<pdp> vec;
    vec.push_back(pdp(0, l.s));
    vec.push_back(pdp(1, l.t));
    // calculate intersections of segment `l` and `border`
    for (Line &b : border) {
        db r = l.intersectRatio(b);
        if (sgn(r) > 0 && sgn(r - 1) < 0) vec.push_back(pdp(r, l.s + (l.t - l.s) * r));
    }
    sort(vec.begin(), vec.end());

    // check visibility of all passed areas
    // because every area is convex, we only need to check the mid-points of neighboring intersections
    for (int i = 1; i < vec.size(); i++) {
        Point p = (vec[i - 1].second + vec[i].second) / 2;
        if (!visible(p, goal)) return 0;
    }
    return 1;
}

// building graph of normal cases
// consider intersections of lines which may change visibility
void build2() {
    // calculate the lines which may change visibility
    vector<Line> border;

    border.push_back(Line(s, m1)); border.push_back(Line(s, m2));
    border.push_back(Line(t, m1)); border.push_back(Line(t, m2));
    for (int i = 0; i < 3; i++) {
        border.push_back(Line(s, a[i]));
        border.push_back(Line(t, a[i]));
    }

    border.push_back(Line(ms, m1)); border.push_back(Line(ms, m2));
    border.push_back(Line(mt, m1)); border.push_back(Line(mt, m2));
    for (int i = 0; i < 3; i++) {
        border.push_back(Line(ms, a[i])); border.push_back(Line(ms, ma[i]));
        border.push_back(Line(mt, a[i])); border.push_back(Line(mt, ma[i]));
    }

    // calculate intersections of `border` and only consider points on the right of mirror
    vector<Point> keys;
    keys.push_back(s); keys.push_back(t);
    for (Line &l1 : border) for (Line &l2 : border) for (Point &p : l1 &l2)
        if (sgn((m2 - m1) * (p - m1)) < 0 && find(keys.begin(), keys.end(), p) == keys.end())
            keys.push_back(p);

    n = keys.size();
    for (int i = 0; i < n; i++) e[i].clear(), v[i].clear(), msk[i].clear();
    // check if segments between two points are valid and calculate visibility
    for (int i = 0; i < n; i++) for (int j = i + 1; j < n; j++) {
        Line l = Line(keys[i], keys[j]);
        // segment intersects with obstacle, can't go from keys[i] to keys[j] directly
        if (!check(l)) continue;
        // calculate if every point on the segment can see start and end points
        int tmp = visible(l, s, border) + visible(l, t, border) * 2;
        e[i].push_back(j); v[i].push_back(l.len()); msk[i].push_back(tmp);
        e[j].push_back(i); v[j].push_back(l.len()); msk[j].push_back(tmp);
    }
}

void solve() {
    scanf("%d", &X);
    scanf("%Lf%Lf%Lf%Lf", &s.x, &s.y, &t.x, &t.y);
    scanf("%Lf%Lf%Lf%Lf", &m1.x, &m1.y, &m2.x, &m2.y);
    for (int i = 0; i < 3; i++) scanf("%Lf%Lf", &a[i].x, &a[i].y);

    mr = Line(m1, m2);
    ms = mr.reflect(s); mt = mr.reflect(t);
    for (int i = 0; i < 3; i++) ma[i] = mr.reflect(a[i]);
    for (int i = 0; i < 3; i++) {
        poly[i] = Line(a[i], a[(i + 1) % 3]);
        mpoly[i] = Line(ma[i], ma[(i + 1) % 3]);
    }

    Line st(s, t);
    if (check(st)) {
        // special case #1: no obstacle on segment between `s` and `t`
        printf("%.12Lf\n", st.len() * (2 * X - 1));
    } else if (X == 1) {
        // special case #2: only one stone
        build1();
        db ans = dijkstra(0);
        if (ans < inf) printf("%.12Lf\n", ans);
        else printf("-1\n");
    } else if (sgn((m2 - m1) * (s - m1)) < 0 && sgn((m2 - m1) * (t - m1)) < 0) {
        // normal case:
        // more than one stone
        // segment between `s` and `t` has obstacle
        // both start and end points are on the right of mirror
        build2();
        db ans = dijkstra(1) + dijkstra(3) * (2 * X - 3) + dijkstra(2);
        if (ans < inf) printf("%.12Lf\n", ans);
        else printf("-1\n");
    } else {
        // special case #3:
        // more than one stone
        // segment between `s` and `t` has obstacle
        // either of both start and end points are on the left of mirror
        printf("-1\n");
    }
}

int main() {
    int tcase; scanf("%d", &tcase);
    while (tcase--) solve();
    return 0;
}